حل المعادلة من الدرجة الثانية في متغير واحد
المعادلة: أ س2 + ب س + حـ = 0 ، س ' ڪ ، أ ، ب ، حـ أعداد مركبة ، أ ≠ (0 ، 0) لها جذران هما:
ــــــــــــــــــــــــ ــــــــــــــــــــــــ
– ب + /\ ب2 – 4 أ حـ – ب – /\ ب2 – 4 أ حـ
س = ـــــــــــــــــــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــــــــــــــــــــــ
2 أ 2 أ
عند حل المعادلة سنحسب الجذر التربيعي لناتج ب2 – 4 أ حـ حسب أحد الطرق السابق ذكرها.
مثال: حل المعادلة س2 – 6س + 15 = 0
الحل: أ = 1 ، ب = – 6 ، حـ = 15 بالتعويض في القانون السابق نجد أن:
ــــــــــــــــــــــــــــــ ــــــــــــــــــــــــــــــ
+ 6 + /\36 – 4×1×15 + 6 – /\36 – 4×1×15
س = ــــــــــــــــــــــــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــــــــــــــــــــــــــ
2 × 1 2 × 1
ــــــــــــــــــــ ـــــــــــــــــــــ
6 + /\36 – 60 6 – /\36 – 60
س = ــــــــــــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــــــــــــ
2 2
ـــــــــــ ـــــــــــــ
6 + /\– 24 6 – /\ – 24
س = ــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــــ
2 2
ـــــ ـــــ
6 + 2/\6 ت 6 – 2/\6 ت
س = ــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــ
2 2
ـــــ ـــــ
س =3 + /\6 ت ، س = 3 – /\6 ت
مثال آخر: حل المعادلة (3 – ت) س2 – 10س + 3(1+ 3ت) = 0
الحل: أ = 3 – ت ، ب = – 10 ، حـ = 3(1+ 3ت) بالتعويض في القانون السابق نجد أن:
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
+ 10 + /\100 – 4×(3 – ت)×3(1+ 3ت) + 10 – /\100 – 4×(3 – ت)×3(1+ 3ت)
س = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ , س = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2 × ( 3 – ت ) 2 × ( 3 – ت )
ــــــــــــــــــــــــــــــــــــــ ــــــــــــــــــــــــــــــــــــــ
10 + /\100 – 72 – 96ت 10 – /\100 – 72 – 96ت
س = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2(3 – ت) 2(3 – ت)
ـــــــــــــــــــــــــ ــــــــــــــــــــــــ
10 + /\28 – 96ت 10 – /\ 28 – 96ت 28 – 96ت = 4(7 – 24ت)
س = ـــــــــــــــــــــــــــــــــــــــــــ , س = ــــــــــــــــــــــــــــــــــــــــــ
2(3 – ت) 2(3 – ت)
ـــــــــــــــــــ ـــــــــــــــــــ
10 + 2/\7 –24ت 10 – 2/\7 – 24ت
س = ــــــــــــــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــــــــــــــــ باختصار 2
2(3 – ت) 2(3 – ت)
ـــــــــــــــــــ ـــــــــــــــــــ
5 + /\7 –24ت 5 – /\7 – 24ت
س = ــــــــــــــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــــــــــــ ................. (1)
3 – ت 3 – ت
نحسب الجذر التربيعي للمقدار 7 – 24ت " نصف 24 = 12 ، 12 = 4 × 3 ، (4)2 – (3)2 = 16 – 9 = 7
7 – 24ت = 16 – 24ت – 9 = (4)2– 24ت + 9ت2 = (4 – 3ت)2 نعوض في (1) مع أخذ الجذر
5 + (4 – 3ت) 5 – (4 – 3ت)
س = ـــــــــــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــــــــــ
3 – ت 3 – ت
5 + 4 – 3ت 5 – 4 +3ت
س = ــــــــــــــــــــــــــــ , س = ـــــــــــــــــــــــــ
3 – ت 3 – ت
9 – 3ت 1 + 3ت 3 + ت
س = ـــــــــــــــــــــ , س = ــــــــــــــــــ × ـــــــــــــــ
3 – ت 3 – ت 3 + ت
3(3 – ت) 10ت
س = ــــــــــــــــــــــ , س = ــــــــــــــــ
3 – ت 9 + 1
س = 3 ، س = ت

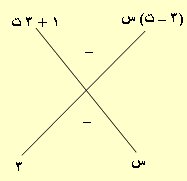
ماذا لو فكرنا بحلها بطريقة أخرى (المقص كما يسمى)
لاحظ صورة المقص
– 3( 3 – ت)س – س(1+ 3ت) = – 9س + 3ت س – 1س – 3ت س = 10س الحد الأوسط
(س – 3)[(3 – ت)س – (1 + 3ت)] = 0
س – 3 = 0 أو (3 – ت)س – (1 + 3ت) = 0
1 + 3ت 3 + ت 10ت 10ت
س = 3 أو س = ــــــــــــــــــ × ـــــــــــــــ = ــــــــــــــ = ــــــــــ
3 – ت 3 + ت 9 + 1 10
س = 3 س = ت
تمارين:
(1) حل المعادلة الآتية حيث س ' ڪ : س2 + 9 ت س – 20 = 0
(2) حل المعادلة س2 + 5 = 0 حيث س ' ڪ
(3) أوجد مجموعة حل المعادلة س3 + 9 س = 0 في ڪ
(4) 2س2– (4 – ت) س + 5 – ت = 0