الصور المختلفة للعدد المركب
عرفنا العدد المركب:
ع = (س ، ص) كصورة هندسية أو ديكارتية ...... (1)
ع = س + ص ت كصورة جبرية ....... (2)
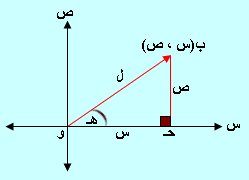
ومن الشكل:
ل طول المتجه و ب ويعرف بمقياس العدد ع (س ، ص)
هـ زاوية تعرف بسعة العدد ع (س ، ص) والقيمة الأساسية لها ' [ 0 ، 2ط [ حيث أن:
ـــــــــــــــــــــــــ
س = ل جتاهـ ، ص = ل حاهـ ، ل = |ع| = /\ س2 + ص2 كمية موجبة
لاحظ حتاهـ = س ÷ ل ، حاهـ = ص ÷ ل
ع = ( ل ، هـ) تعرف بالصورة القطبية للعدد المركب ....... (3)
ع = س + ص ت = ل حتاهـ + ل حاهـ × ت = ل ( حتاهـ + ت حاهـ ) من (2)
ع= ل ( حتاهـ + ت حاهـ ) تعرف بالصورة المثلثية للعدد المركب ...... (4)
تنبيه: من الواضح أنه يمكن الحصول على أي صورة للعد المركب من صورة أخرى
العدد المركب ع = 3 + 3ت هو في صورة جبرية ويكون:
ع = (3 ، 3) في الصورة الهندسية أو الديكارتية
ـــــــــــ ــــ ـــــ ــــ ــــ ـــــ
ل = |ع| = /\9+9 = 3 /\2 ، حتاهـ = 3 ÷ 3/\2 = 1÷ /\2 ، حاهـ = 3÷ 3/\2 = 1÷ /\2 ومنها هـ = 45ه (النسب حا، حتا موجبة)
ـــــ
ع = (3/\2 ، ط/4) الصورة القطبية للعدد المركب
ــــ
ع = 3/\2 ( حتا(ط/4) + ت حا(ط/4) ) الصورة المثلثية للعدد المركب