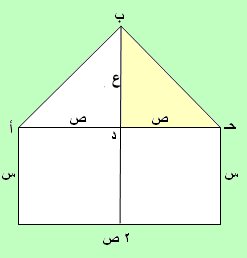
من الشكل المبين:
بعدا المستطيل س ، 2 ص ، ع للمثلث = 0.375 × 2 ص = 0.75 ص ( ع = 0.75 ص )
من المثلث ب د حـ القائم في د نحسب طول ب حـ باستخدام نظرية فيثاغورث
(ب حـ)2 = (ب د)2 + (حـ د)2 = (0.75 ص)2 + ص2 = 0.5625 ص2 + ص2 = 1.5625 ص2
ب حـ = 1.25 ص
←
(1) ( طول ضلع المثلث )
محيط النافذة = 9
2 س + 2 ص + 2 × 1.25 ص = 9
2 س + 2 ص + 2.5 ص = 9
2 س + 4.5 ص = 9
2س = 9 − 4.5 ص
س = 4.5 − 2.25 ص ← (2)
مساحة النافذة السامحة لنفاذ الضوء (م) = س × 2 ص + 0.5 × 2 ص × 0.75 ص
م = ( 4.5 − 2.25 ص ) × 2 ص + 0.75 ص2 ( عوضنا عن س من (2) )
م = 9 ص − 4.5 ص2 + 0.75 ص2
م = 9 ص − 3.75 ص2
مــ = 9 − 7.5 ص ( مــ = 0 لكون م عظمى )
0 = 9 − 7.5 ص
ص = 1.2 متر ومنها عرض المستطيل 2.4 متر
في (2) نجد أن: س = 4.5 − 2.25 × 1.2 = 4.5 − 2.7 = 1.8 متر
في (1) نجد أن: طول ضلع المثلث ب حـ = 1.25 × 1.2 = 1.5 متر
الأبعاد المطلوبة هي : 1.8، 2.4 متر وطول ضلع المثلث 1.5 متر