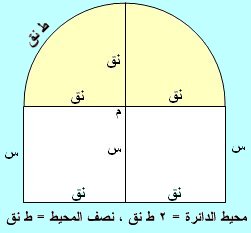
من الشكل المبين:

 بعدا المستطيل س ، 2 نق حيث نق نصف قطر الدائرة التي مركزها م وتكون مساحة المستطيل س × 2 نق = 2 س نق ، ومساحة نصف الدائرة 0.5ط نق² في حين محيط نصف الدائرة = ط نق، والضوء يدخل خلال المساحة كاملة للمستطيل و نصف الدائرة.

المحيط ثابت أي:

2 س + 2 نق + ط نق = ث    ← (1)  

حيث أن:  ث الثابت، 2 س + 4 نق محيط المستطيل ، ط نق نصف محيط الدائرة

بإيجاد س بدلالة نق أي:

2 س = ث − 2 نق − ط نق   ← (2)  

المساحة القابلة لدخول الضوء:

م = س × 2 نق + 0.5 ط نق²

م = 2 س نق + 0.5 ط نق²  ← (3)  

بالتعويض من (2) في (3) يكون:

م = ( ث − 2 نق − ط نق ) نق + 0.5 ط نق²

  = ث نق − 2 نق² − ط نق² + 0.5 ط نق²

  = ث نق − 2 نق² − 0.5 ط نق²  بالاشتقاق بالنسبة إلى نق

م^ــ = ث − 4 نق − ط نق ، ومن حيث م أكبر ما يمكن فإنَّ م^ــ = 0 أي أن:

صفر = ث − 4 نق − ط نق

ث = 4 نق + ط نق  ← (4)  

من (4) في (1)

2 س + 2 نق + ط نق = 4 نق + ط نق

2 س = 2 نق

س =  نق

عرض المستطيل ( 2 نق ) = ارتفاع النافذة الكلي ( س + نق = نق + نق = 2 نق )

للتأكد نوجد المشتقة الثانية للمساحة لتبيان أنها سالبة للدلالة على وجود القيمة العظمى للمساحة

م^// = 0 − 8 − ط  = كمية سالبة أي القيمة عظمى وهذا يدلل على صحة الإجابة

حل آخر: بعد تكوين المعادلات كما سبق في الحل السابق نقول:

2 س + 2 نق + ط نق = ث    ← (1)  

م = 2 س نق + 0.5 ط نق²  ← (3)  

نشتق كل من (1) ،  (3) بالنسبة إلى نق فيكون

2 س^ــ + 2 + ط = صفر   من (1) والاشتقاق  ومنها  2 س^ــ = − 2 − ط

صفر = 2 س × 1 + 2 س^ــ نق + ط نق   من (3) والاشتقاق،  لاحظ مشتقة حاصل ضرب دالتين ( 2 س نق )

2 س + 2 س^ــ نق + ط نق = صفر

بالتعويض عن  2 س^ــ   بـ ( − 2 − ط  ) يكون:

2 س + ( − 2 − ط ) نق + ط نق = 0

2 س − 2 نق − ط  نق + ط نق = 0

2 س = 2 نق

س =  نق

عرض المستطيل ( 2 نق ) = ارتفاع النافذة الكلي ( س + نق = نق + نق = 2 نق )

للتأكد نوجد المشتقة الثانية للمساحة لتبيان أنها سالبة للدلالة على وجود القيمة العظمى للمساحة

م^// = 0 − 8 − ط  = كمية سالبة أي القيمة عظمى وهذا يدلل على صحة الإجابة