في المثلث هـ ب ز القائم في ب ، ب ى عمودي على هـ و قطعة أرض على شكل قطعة دائرية طول قاعدتها 96 متر وارتفاعها 32 متر يراد إقامة بناء على هذه القطعة الدائرية قاعدته على شكل مستطيل، أوجد أبعاد أكبر قاعدة للبناء.
الحــل :
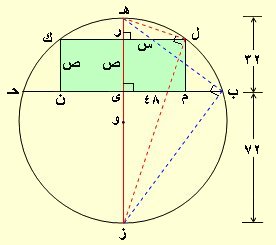
هندسة الشكل ضرورية هنا وخاصة معرفة القطعة الدائرية التي تنشأ من رسم وتر الدائرة فتتولد قطعة صغرى وأخرى كبرى ما لم يمر الوتر بمركز الدائرة(حيث يكون قطر) ففي الشكل المرفق الوتر ب حـ قسم الدائرة إلى قطعتين صغرى فوقه وكبرى تحته وإن ارتفاع القطعة الصغرى هو دهـ=32 متر في حين طول قاعدة القطعة يساوي طول الوتر ب حـ = 96 متر وقاعدة البناء هي المستطيل ل م ن ك المطلوب اكبر مساحة له(ح) سنفرض أن م ن =2س ، ل م = ص ، وهـ عمودي على كل من الوتر ب حـ ، الوتر ل ك فهو ينصفهم(و مركز الدائرة) وزاويتي ل ، ب قائمتان لكونهم مرسومتان على القطر(أو في نصف دائرة) ، ل ر= س، رهـ =32 – ص ، طول ب حـ=96 متر فإن ب ى=48 متر
في المثلث هـ ب ز القائم في ب ، ب ى عمودي على هـ و
(ب ى)2 = هـ ى × ى ز نتيجة لنظرية فيثاغورث أو من التشابه
48 × 48 = 32 × ى ز
ى ز = 72
في المثلث ل هـ ز القائم في ل ، ل ر عمودي على هـ ز
(ل ر)2= هـ ر × ر ز نتيجة لنظرية فيثاغورث أو من التشابه
س2= ( 32 – ص ) ( 72 + ص )
س2= 2304 – 40 ص – ص2
والمساحة ح أكبر ما يمكن أي ح¯ = صفر وهذا يعني أما البسط = صفر أو المقام = ¥ وعليه يكون :
2304 × 2 ص – 120 ص2 – 4 ص3 = 0
4 ص(1152 – 30 ص – ص2) = 0
ص = 0 أو 1152 – 30 ص – ص2 = 0 (استخدام القانون العام لحل المعادلة بعد القسمة على – 1(إن شئت)
ص = 0 أو ص = – 52.11 أو ص = 22.11 والقيم 0 ، – 52.11 غير عملية فتكون ص = 22.11
عند ص < 22.11 (مثل 2) نجد أن ح¯ قيمة موجبة
عند ص > 22.11 (مثل 22.2) نجد أن ح¯ قيمة سالبة
والمساحة ح أكبر ما يمكن أي ح¯ = ¥ وعليه يكون المقام = صفر أي القيمة تحت الجذر التربيعي = صفر
2304 ص2 – 40 ص3 – ص4 = 0
ص2(2304 – 40 ص – ص2) = 0
ص = 0 أو ص = – 72 أو ص = 32 وكلها قيم غير عملية
إذن قيم ص = 22.11 القيمة الوحيدة التي تعطي أكبر ما يمكن وبالتعويض في (1) للحصول على قيمة س يكون :
س = 30.51
الأبعاد المطلوبة هي 30.51 ، 22.11 متر