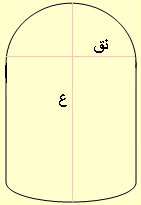
 بفرض نق نصف قطر القاعدة ، ع ارتفاع الخزان (لاحظ الشكل)
بفرض نق نصف قطر القاعدة ، ع ارتفاع الخزان (لاحظ الشكل)يراد عمل خزان للمياه اسطواني دائري قائم لسع 300 ط متر مكعب من الماء، وعمل له غطاء على شكل نصف كرة مجوفة وكان تكاليف المتر المربع من القاعدة 40 ريال، ومن الجوانب 20 ريال، ومن الغطاء 10 ريال، فأوجد أبعاد الخزان لكي تكون التكاليف أقل ما يمكن.
الحـل :
 بفرض نق نصف قطر القاعدة ، ع ارتفاع الخزان (لاحظ الشكل)
بفرض نق نصف قطر القاعدة ، ع ارتفاع الخزان (لاحظ الشكل)
حجم الاسطوانة = ط نق2ع
300 ط = ط نق2ع وبحذف ط ¹ 0
300 = نق2ع نحصل منها على متغير(ع) بدلالة الآخر(نق)
ع = 300 نق–2 ............... (1)
التكاليف(ت) = تكاليف القاعدة + تكاليف الجوانب + تكاليف نصف سطح الكرة(الغطاء)
التكاليف(ت) = ط نق2 × 40 + 2 ط نق ع × 20 + 2 ط نق2 × 10
التكاليف(ت) = 60 ط نق2 + 40 ط نق ع .............. (2)
بالتعويض من (1) في (2) عن قيمة ع للحصول على معادلة التكاليف بمتغير واحد هو نق
ت = 60 ط نق2 + 40 ط نق × 300 نق–2
ت = 60 ط نق2 + 12000 ط نق–1 بالاشتقاق بالنسبة إلى نق
ت¯ = 120 ط نق – 12000 ط ، ت أقل ما يمكن يعني ت¯= 0
صفر= 120 ط( نق – 10) ، ط ¹ 0
نق = 10متر
نوجد المشتقة الثانية لمعرفة النهاية في حالة نق = 10
ت// = 120 ط = كمية موجبة أي توجد نهاية صغرى للدالة ت (أقل ما يمكن)
وفي (1) ع = 300 ÷ 100 = 3 متر
أبعاد الخزان المطلوبة هي 10 ، 3 متر
تنبيه : المشتقة الأولى للدالة ت = ¥ عندما نق = 0 مقدار ليس له قيمة عملياً