أوجد أكبر حجم لمخروط يمكن قطعه
من كرة نصف قطرها 18سم ورأسه على سطح الكرة ويمس محيط قاعدته سطح الكرة.
الحـل :
 هندسة
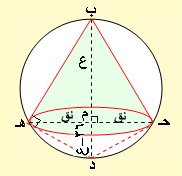
الشكل ضرورية هنا لإيجاد العلاقة بين المتغيرين نق ، ع والتي يمكن الحصول عليها من
نتيجة لنظرية فيثاغورث أو من تقاطع وترين في دائرة فحسب نتيجة فيثاغورث في المثلث
هـ ب د القائم في هـ لكون ب د قطر حيث ب م ارتفاع المخروط ، م حـ نصف قطر المخروط
وعليه يكون :
هندسة
الشكل ضرورية هنا لإيجاد العلاقة بين المتغيرين نق ، ع والتي يمكن الحصول عليها من
نتيجة لنظرية فيثاغورث أو من تقاطع وترين في دائرة فحسب نتيجة فيثاغورث في المثلث
هـ ب د القائم في هـ لكون ب د قطر حيث ب م ارتفاع المخروط ، م حـ نصف قطر المخروط
وعليه يكون :
(حـ م)2 = م ب × م د
نق2 = ع (36 – ع)
نق2 = 36 ع – ع2
.......... (1)
أو من تقاطع الوتران ب د ، حـ هـ في م فيكون
م حـ × م هـ = م ب × م د
نق × نق =
ع × (36 – ع)
نق2
= 36 ع – ع2 وهي
نفس المعادلة السابقة
والآن نوجد العلاقة الأخرى التي تمثلت في حجم المخروط
ليكون نهاية عظمى
ح =
⅓ ط نق2ع
.......... (2)
ح =
⅓ ط (36 ع
– ع2)ع
ح =
12ط ع2–
⅓ ط ع3
ح¯=
12 ط ع – ط
ع2 بوضع
ح¯=
0 لكون ح نهاية عظمى
0 = ط ع(12 – ع)
ع = 0
(مرفوض) أو ع = 12 سم
في(1) : نق2= 36 × 12
– 144 = 12 × 24 = 288
في
(2) : ح = ⅓
ط × 288 × 12 = 1152ط سم3
لاحظ : ح// = 12ط – 2 ط ع
ح// = 12ط – 2 ط × 12= كمية سالبة (نهاية عظمى)
 هندسة
الشكل ضرورية هنا لإيجاد العلاقة بين المتغيرين نق ، ع والتي يمكن الحصول عليها من
نتيجة لنظرية فيثاغورث أو من تقاطع وترين في دائرة فحسب نتيجة فيثاغورث في المثلث
هـ ب د القائم في هـ لكون ب د قطر حيث ب م ارتفاع المخروط ، م حـ نصف قطر المخروط
وعليه يكون :
هندسة
الشكل ضرورية هنا لإيجاد العلاقة بين المتغيرين نق ، ع والتي يمكن الحصول عليها من
نتيجة لنظرية فيثاغورث أو من تقاطع وترين في دائرة فحسب نتيجة فيثاغورث في المثلث
هـ ب د القائم في هـ لكون ب د قطر حيث ب م ارتفاع المخروط ، م حـ نصف قطر المخروط
وعليه يكون :