التفاضـل

القسم الثامن

المعدلات الزمنية المرتبطة

    في المسائل العملية تكون المتغيرات متوقفة في تغيرها على الزمن كتمدد فقاعة كروية محتفظ بانتظام بشكلها فكلاً من نصف قطرها نق وحجمها ح يتوقف ازدياده على ازدياد الزمن طالما العلاقة بين ح ، نق  ثابتة فإجراء عملية التفاضل بالنسبة للزمن على هذه العلاقة(ح، نق) فتنتج معادلة تربط المعدلين الزمنيين لهاتين الكميتين(ح ، نق) والأمثلة التالية توضح هذا.

مثال(1)

    يضغط غاز داخل بالون كروي بمعدل 1540 سم³ / ث أوجد معدل الزيادة في كل من نصف القطر ، مساحة السطح الكروي للبالون في اللحظة التي يكون فيها نصف القطر 7 سم ( ط = 22 ÷ 7 ، حجم الكرة = (4 /3) ط نق³ )

الحــل :

    ح = (4 /3) ط نق³   ( حجم الكرة )

    ح¯ = 4 ط نق² نق¯  حيث ح¯  مشتقة ح بالنسبة للزمن أو معدل التغير في الحجم ، نق¯ معدل التغير في نصف القطر(مشتقة نق بالنسبة للزمن)

   1540 = 4 × (22 ÷7) × 7 × 7 نق¯

    نق¯  = 2.5 سم / ث  وهو معدل تغير نق أو السرعة إن شئت

    م = 4 ط نق² ( مساحة سطح الكرة )

    م¯ = 4 ط × 2 نق نق¯            م¯  هي معدل الزيادة في المساحة عند أي لحظة

    م¯ = 4 × (22 ÷ 7) × 2 × 7 × 2.5    م¯  هي معدل الزيادة في المساحة عندما نق = 7 سم

    م¯ = 440 سم² / ث

مثال(2)

     ضلع مربع يزداد بانتظام بمعدل 0.1 سم في الثانية فبأي معدل تزداد المساحة عندما يكون طول ضلع المربع 10 سم

الحـل :

    م = ل²    حيث م مساحة المربع الذي طول ضلعه ل وكلاهما متغير

    م¯ = 2 ل ل¯   ل¯ معدل التغير في نصف القطر ، م¯ معدل التغير في المساحة(عند أي لحظة)

    م¯ = 2 × 10 × 0.1    م¯ معدل التغير في المساحة(عند ل = 10 سم )

    م¯ = 2 سم² / ث

مثال(3)

    جسم مكون من اسطوانة دائرية قائمة يعلوها نصف كرة ، وكان نصف قطر قاعدتيهما المشتركة يزداد بمعدل 0.6 سم / ث وارتفاع الاسطوانة يزداد

 بمعدل 0.9 سم / ث فأوجد معدل زيادة حجم الجسم عندما يكون نصف القطر يساوي 15 سم وارتفاع الاسطوانة 30 سم ( حجم الاسطوانة= ط نق²ع)

الحـل :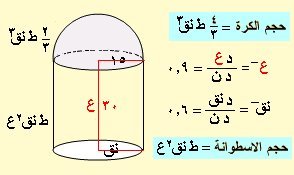

    بفرض ارتفاع الاسطوانة ع ونصف القطر نق عند أي لحظة ( لاحظ الشكل )

    ح = ط نق²ع + (2 ÷3) ط نق³   ح حجم الجسم = ح للاسطوانة + ح لنصف الكرة

    ح¯ = ط ( 2 نق نق¯ ع + نق² ع¯ ) + 2 ط نق² نق¯  اشتقاق حاصل ضرب نق²ع

    ح¯ = ط ( 2 × 15 × 0.6 × 30 + 225 × 0.9 ) + 2 ط × 225 × 0.6

    ح¯ = ط ( 2 × 15 × 0.6 × 30 + 225 × 0.9 + 2 × 225 × 0.6)

    ح¯ = 1012.5 ط     وبفرض ط = 3.14 يكون المطلوب

    ح¯ =  3179.25

مثال(4)

    سفينتان تبدآن بالسير من نقطة واحدة فالأولى تبدأ في الساعة العاشرة صباحاً متجهة نحو الشرق بمعدل 12 كم / ساعة والثانية تبدأ في الساعة الحادية عشرة صباحاً متجهة نحو الجنوب بمعدل 18 كم / ساعة فبأي معدل تبتعدان إحداها عن الأخرى عند الساعة 12 ظهراً ؟

الحـل :

    يجب أن نعرف أن اللفظ بمعدل 9 أي السرعة 9       

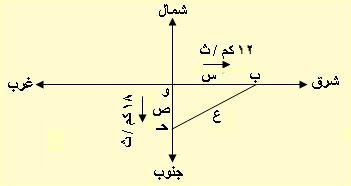
    الشكل يوضح نص المسألة

    عند اللحظة ن يكون ب موضع السفينة الأولى على بعد س من و نقطة الابتداء والسفينة الثانية تكون عند حـ على بعد ص من و نقطة الابتداء ونفرض البعد بين السفينتين ب حـ = ع

نحسب البعد ع (ب حـ) حيث المسافة = ع × ن

السفينة الأولى عند الساعة 12 قطعت مسافة س = 12 × 2 = 24 كم

السفينة الثانية عند الساعة 12 قطعت مسافة ص = 18 × 1= 18 كم

وبناء على نظرية فيثاغورث

        ع² =  س² +  ص² .................... (1)

        ع² =  576 + 324 = 900

        ع = 30 كم

    باشتقاق المعادلة (1)

    2 ع ع¯ = 2 س س¯ + 2 ص ص¯

       ع ع¯ =  س س¯ +  ص ص¯

     30 ع¯ = 24 × 12 + 18 × 18

     30 ع¯ = 492

          ع¯ = 16.4 كم / ساعة عند الساعة 12 ظهراً

مثال(5)

    تتحرك نقطة على المنحنى س² + ص² – 4 س – 6 ص – 7 = 0 وعندما كانت فوق النقطة ( – 2 ، 5 ) كانت سرعتها في اتجاه محور السينات( أي س¯ ) تساوي – 2 احسب سرعتها عندئذٍ في اتجاه محور الصادات( أي ص¯ ).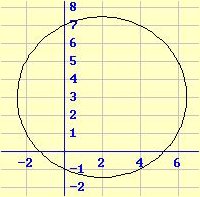

الحـل :

    س² + ص² – 4 س – 6 ص – 7 = 0 بالاشتقاق بالنسبة للزمن

    2 س س¯ + 2 ص ص¯ – 4 س¯ – 6 ص¯ = 0 بالتعويض عن س ، ص ، س¯

    2 × – 2 × – 2  + 2 × 5 ص¯ – 4 × – 2  – 6 ص¯ = 0

    8 + 10 ص¯ + 8 – 6 ص¯ = 0

    16 + 4 ص¯ = 0  بالقسمة على 4

    4 + ص¯ = 0

    ص¯ = – 4     وهي السرعة المطلوبة في الاتجاه السالب لمحور الصادات

مثال(6)

    مكعب من الثلج بدأ في الذوبان محتفظاً بشكله كمكعب دوماً فإذا كان طول الضلع للمكعب يتناقص بمعدل 2 سم / ث في اللحظ التي ينقص فيها الحجم بمعدل 12 سم³ / ث.أوجد طول ضلع المكعب عند تلك اللحظة

الحـل :

    ح = ل³     ح حجم المكعب الذي طول ضلعه ل

    ح¯ = 3 ل ل¯       من اشتقاق المعادلة السابقة بالنسبة للزمن

    –12 = 3 ل × –2    إشارة –  للفظ التناقص

    ل = 2 سم

لاحظ : المكعب مجسم طوله = عرضه = ارتفاعه = ل وأوجهه مربعات أي منها قاعدة له

مثال(7)

    إناء على شكل مخروط دائري قائم نصف قطر قاعدته 7 سم وارتفاعه 28 سم في وضع رأسي وقاعدته لأعلى ومملوء بالماء. يتسرب منه الماء من فتحة ضيقة عند رأسه بمعدل 22سم³ / ث ؛ أوجد المعدل الذي يهبط به سطح الماء عندما يكون الماء على عمق 24 سم من سطح الإناء

( ط = 22÷ 7  ، ح =  ط نق²ع / 3)

الحـل :

حل آخر :

الفكرة : نشتق كل من العلاقتين 1) علاقة نق ، ع   2) علاقة ح، نق، ع ومن الأولى نعوض في الثانية
من تشابه المثلثين ب حـ د ، ب هـ د :  نق ÷ 7 = ع ÷ 28 ومنها

نق = ¼ ع ....... (1)  نشتق فنحصل على
نق¯ = ¼ ع¯ ... (2)

ح = (1 /3) ط نق2 ع  نشتق فنحصل على
ح¯ = (ط / 3) [ نق2 ع¯ + 2 نق نق¯ ع ] ....... (3)
عند اللحظة المطلوبة يكون : ع = 28 -24 = 4 وعليه يكون نق = ¼ × 4 = 1 ( من المعادلة(1) ) وبالتعويض في (3)
–22 = (22 ÷ 3×7) [ 1 × ع¯ + 2 × 1 × ( ¼ ع¯ × 4]
–22 = (22 ÷ 3×7) [ ع¯ + 2ع¯]
– 1 = 22 × 3 ع¯ ÷ 3 × 7
ع¯ = – 7 سم / ث معدل هبوط الماء ( إشارة – تعني هبوط أو نقص )

تنبيه : يمكن إعطاء المسألة بصورة أخرى بأن يكون المخروط أسفل حنفية ماء حيث يتساقط الماء من الحنفية بمعدل ثابت ويكون المطلوب معدل ارتفاع الماء في المخروط ، وقد نجمع الأمرين بأن يُصب الماء في المخروط من أعلى بمعدل 9 سم³ في الثانية في حين يتسرب في نفس الوقت منه الماء بمعدل 4 سم³ في الثانية فيكون معدل الزيادة 9 – 4 = 5 سم³ في الثانية ونستمر في الحل كما في المثال ، هذا وينطبق القول هذا على إناء بشكل اسطواني .

مثال(8) :
صفيحة رقيقة من المعدن على شكل مربع تتمدد بالحرارة ، فإذا كان معدل زيادة محيطها 0.25 سم / ث فاحسب معدل زيادة مساحتها عندما يكون طول ضلعها 32 سم
الحـل :
المحيط ح = 4 ل ، المساحة م = ل2 حيث ل طول ضلع الصفيحة المربعة الشكل
باشتقاق معادلة المحيط بالنسبة للزمن يكون
ح¯ = 4 ل¯
0.25 = 4 ل¯
ل¯ = 0.0625
باشتقاق معادلة المساحة بالنسبة للزمن يكون
م¯ = 2 ل ل¯
= 2 × 32 × 0.0625
م¯ = 4 سم / ث2

تمرين (1)

    ضلعان من مثلث يزداد كل منهم بمعدل 0.3 سم في الثانية ، والزاوية المحصورة بينهم تزداد بمعدل 0.2 من زاوية نصف قطرية في الثانية ، بأي معدل تتغير مساحة المثلث عند اللحظة التي يكون فيها كل ضلع من أضلاع المثلث 30 سم (مساحة أي مثلث تساوي نصف حاصل ضرب أي ضلعين فيه × جيب الزاوية المحصورة بينهما ، والمثلث المتساوي الأضلاع كل من زواياه = 60 درجة أي ط ÷ 3  ، مشتقة حاس هي حتاس )

تمرين (2)

    وعاء على شكل مخروط دائري قائم ارتفاعه 7 قدم ، ونصف قطر قاعدته 3 قدم وضع بحيث يكون محوره رأسياً ورأسه لأسفل فإذا صب فيه مياه بمعدل 10 أقدام مكعبة في الدقيقة فأوجد معدل ازدياد عمق الماء

    (1) عندما يكون عمق المياه 4 أقدام

    (2) عندما يكون الوعاء مشتمل على 60 قدماً مكعباً من المياه         ( الجواب 1.083 ، 0.377 )

تمرين (3)

   يسير رجل طوله 6 أقدام بسرعة 6 قدم / ث مبتعداً عن قائم مصباح ارتفاعه 10 قدم والمطلوب إيجاد معدل ازدياد ظل الرجل . وإذا كانت ى هي الزاوية التي يميل بها المستقيم الواصل بين أعلى نقطة من رأس الرجل وبين قمة المصباح على الأرض عندما يبعد الرجل عن قائم المصباح بمسافة قدرها ل من الأقدام فأثبت أن ل = 4 طتاى ، ثم ابحث من ذلك عن معدل نقص ى عندما يبعد الرجل عن المصباح بمسافة 8 أقدام.