التفاضـل

القسم التاسع1

 المشتقة الأولى للدوال غير الجبرية

    بالنسبة للدوال الدائرية العكسية الستة حا^–1س، حتا^–1س، طا^–1س، طتا^–1س، قا^–1س، قتا^–1س سيكون اشتقاق أي منها بعد وضعها في صورة جديدة ولنأخذ دالة الجيب كمثال حيث سنكتبها بالصورة س = حا ص ومن ثم نشتق بالنسبة إلى ص وبعد ذلك نوجد المشتقة المطلوبة، هذا ويجب أن نهتم بقوانين حساب المثلثات ومن أهمها

•  حا² س + حتا² س = 1   ومنها     حا² س = 1 –  حتا² س    ،     حتا² س  = 1 –  حا² س

•  قا² س –  طا² س = 1     ومنها      قا² س = 1 +  طا² س     ،     طا² س = قا² س – 1

•  قتا² س –  طتا² س = 1     ومنها      قتا² س = 1 +  طتا² س ،     طتا² س = قتا² س – 1

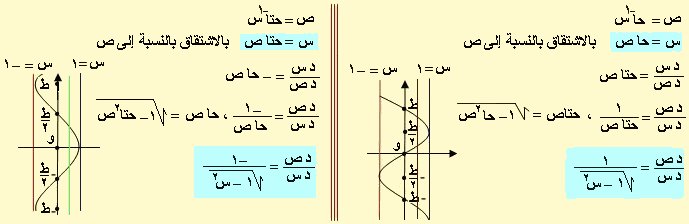
سابعاً : حا^–1س ، حتا^–1س

    من منحنى الدالة نجدها متعددة القيم فإذا أعطينا للمتغير س قيمة مثل 0.5 فالدالة تأخذ قيماً متعددة مناظرة والمستقيم س = 0.5 يقطع المنحنى في عدة نقط كما هو مبين بالرسم ، ولإيجاد المشتقة نقول :

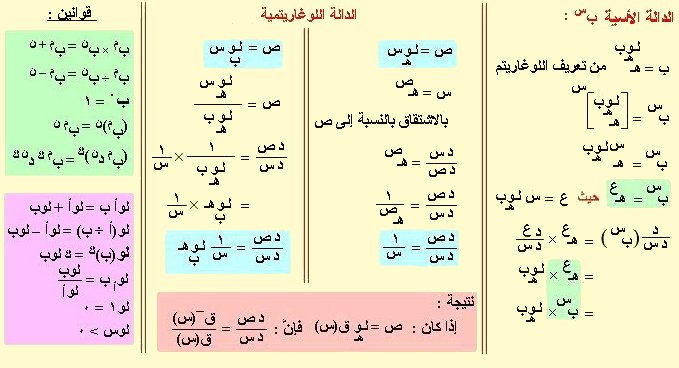
الدالة الأسية  _هـ^س

        من المعلوم أن _هـ^س = 1 + س + س²÷ 1×2 + س³÷ 1×2×3 + س⁴÷ 1×2×3×4 + ... ¥

وعلى فرض أن هذه المتسلسلة متقاربة وهو صحيح فبالاشتقاق نحصل على الدالة نفسها حيث يكون

    (_هـ^س )¯ = 0 + 1+ 2س ÷ 1×2 + 3س²÷ 1×2×3 + 4س³÷ 1×2×3×4 + ... ¥

   (_هـ^س )¯ = 1+ 2س ÷ 1×2 + 3س²÷ 1×2×3 + 4س³÷ 1×2×3×4 + ... ¥

  (_هـ^س )¯ = _هـ^س  أي مشتقتها نفس الدالة وهي خاصية تمتاز بها هذه الدالة وتمتاز بخاصية أخرى طول تحت المماس عند أي نقطة = 1 دوماً ويتضح ذلك من الرسم المرفق حيث أن

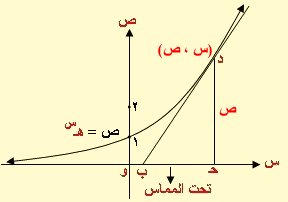
ص = _هـ^س

ص¯ = _هـ^س  وهو ميل المماس

أي ميل المماس = ص

ولكن الميل هو ظل الزاوية أي طا د ب حـ = ص

لكن طا د ب حـ = د حـ ÷ ب حـ = ص ÷ ب حـ

أي ص = ص ÷ ب حـ

ب حـ = 1

طول تحت المماس = 1 مهما كان موضع النقطة د