التفاضـل
القسم التاسع
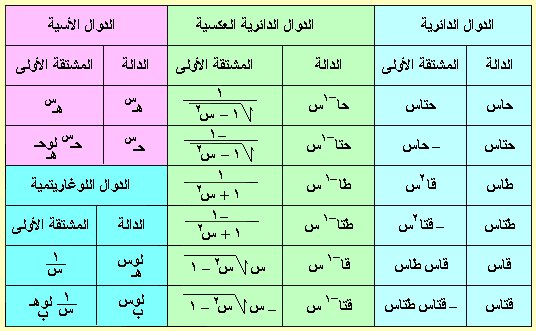
المشتقة الأولى للدوال غير الجبرية
أولاً : حاس
رسم منحنى الدالة مبين بالشكل حيث
– 1
³
حا س
³
1
د(س) = حا س .............. (1)
د(س + هـ) = حا( س + هـ )
........... (2) بإحداث تغير صغير جداً قدره هـ
وبالطرح (1) ، (2)
ت(هـ) = حا( س +
هـ) – حا س حيث ت(هـ) =
د(س + هـ) – د(س)
وبتطبيق قوانين حساب المثلثات نحصل
على
ت(هـ) = [حا( س + هـ) – حا س]
ت(هـ) = 2 حتا½(س
+ هـ + س) حا½(س + هـ –س)
ت(هـ) = 2 حتا½(2س
+ هـ) حا½(هـ)
وبالقسمة على هـ نحصل على م(هـ) وهو
متوسط معدل التغير
م(هـ) = [2 حتا½(2س
+ هـ) حا½(هـ)] ÷ هـ=
حتا½(2س
+ هـ) × [حا½(هـ) ÷
½هـ] وبأخذ
النهاية عندما هـ تؤول للصفر
م(هـ) =
حتا½×2س
× 1 لأن نهاية [حا½(هـ)
÷ ½هـ] = 1 عندما
½هـ تؤول للصفر
د¯(س)
= حتاس
نتيجة :
د(س) = حا[ق(س)] فإن :
د¯(س)
=
حتا[ق(س)] × ق¯(س)
نتيجة : د(س) = حان[ق(س)] فإن :
د¯(س)
=
ن [حان – 1ق(س)] ×
حتاق(س) × ق¯(س)
مثال(1)
:
أوجد المشتقة الأولى للدالة ص = س2 حا س
الحــل
:
مشتقة حاصل ضرب دالتين (س2 ،
حاس) = الدالة الأولى × مشتقة الدالة الثانية + مشتقة الدالة الأولى × الدالة
الثانية
ص¯
= س2حتاس + 2 س حا س
مثال(2)
:
إذا كانت د(س) = حا( 2 س + 3 ) فأوجد د¯(س)
عند س = 43.5ه
الحــل
:
د¯(س)
= حتا(2 س + 3) × 2 مشتقة الدالة الدائرية
× مشتقة الزاوية
د¯(س)
= 2 حتا(2 س + 3) عند أي قيمة للمتغير س
د¯(43.5ه)
= 2حتا( 2 × 43.5ه + 3) = 2 حتا90ه = 2 × 0 = 0
مثال(3)
:
أوجد المشتقة الأولى للدالة ق(س) = 3
حا3(2 س2 + 3س +1)
الحـل :
ق¯(س)
= 3 × 3[حا2(2
س2 + 3س +1)] × [حتا(2 س2 + 3س +1)]
× ( 4 س + 3)
ق¯(س)
= 9(4 س + 3)حا2(2
س2 + 3س +1)حتا(2 س2 + 3س +1)
مثال(4)
:
أوجد المشتقة الأولى للدالة ص = حا2س حتا2س
الحـل :
يمكن حل المسألة على أساس حاصل ضرب دالتين ولكن لدينا قانون
حا2س = 2 حاس حتاس وهذا يقودنا لجعل المسألة في جيب الزاوية
ص = 4 حا2س حتا2س ÷ 4
ص = ¼
حا2(2س)
ص¯
= ¼ × 2 حا2س × حتا2س × 2
ص¯
= حا2س × حتا2س
ص¯
= ½ حا4س
ثانياً : حتاس
د(س) = حتا س .............. (1)
د(س + هـ) = حتا( س + هـ )
........... (2) بإحداث تغير صغير جداً قدره هـ
وبالطرح (1) ، (2)
ت(هـ) = حتا( س +
هـ) – حتا س حيث ت(هـ) =
د(س + هـ) – د(س)
التغير في الدالة
وبتطبيق قوانين حساب المثلثات نحصل
على
ت(هـ) = [حتا( س + هـ) – حتا س]
ت(هـ) = –2 حا½(س
+ هـ + س) حا½(س + هـ –س)
ت(هـ) = –2 حا½(2س
+ هـ) حا½(هـ)
وبالقسمة على هـ نحصل على م(هـ) وهو
متوسط معدل التغير
م(هـ) = [–2 حا½(2س
+ هـ) حا½(هـ)] ÷ هـ=
– حا½(2س
+ هـ) × [حا½(هـ) ÷
½هـ] وبأخذ
النهاية عندما هـ تؤول للصفر
م(هـ) =
–
حا½×2س
× 1 لأن نهاية [حا½(هـ)
÷ ½هـ] = 1 عندما
½هـ تؤول للصفر
د¯(س)
=
–
حاس
نتيجة :
د(س) = حتا[ق(س)] فإن :
د¯(س)
= –
حا[ق(س)] × ق¯(س)
نتيجة : د(س) = حتان[ق(س)] فإن :
د¯(س)
=
ن [حتان – 1ق(س)] ×
– حاق(س) × ق¯(س)
وهذا ينطبق على باقي الدوال الدائرية
مثال(1)
:
إذا كانت س حا ص + ص حتا س
= 0 فأوجد ص¯
الحـل :
بإجراء الاشتقاق لحاصل ضرب دالتين
على حديّ المعادلة
س حتا ص × ص¯
+ 1× حا ص + ص × – حاس + ص¯
حتا س =0
ص¯(
س حتا ص + حتا س) – ( ص حا س – حا ص ) = 0
ص¯
= ( ص حا س – حا ص ) ÷ ( س حتا ص + حتا س)
مثال(2) :
إذا كانت د(س) = 2 حتا2س
– 1 فأوجد د¯(45ه)
الحـل :
د¯(س)
= 2 × 2 حتا س × (– حا س)
د¯(س)
= –4 حتا س حا س يمكن وضعها بالصورة
د¯(س)
= –2 حا2س حيث حا 2س = 2 حاس حتاس
د¯(45ه)
= –2 حا2×45ه
د¯(45ه)
= –2 حا90ه
د¯(45ه)
= –2 × 1
د¯(45ه)
= –2
حـل آخر
د(س) = حتا2س
لأن حتا2س = حتا2س
– حا2س = 2 حتا2س – 1 = 1 – 2 حا2س
د¯(س)
= – حا2س × 2
د¯(س)
= –2 حا2س
د¯(45ه)
= –2 حا90ه = – 2 × 1 = – 2
ثالثاً : طا س
د(س) = طا س يمكن البرهنة بنفس الطريقة
السابقة ولكن سنستخدم الطريقة التاللية
د(س) = حا س ÷ حتا س
بالاشتقاق كقسمة دالتين
د¯(س)
= [ حتا س × حتا س – حا س × – حا س ] ÷ حتا2س
د¯(س)
= [ حتا2س + حا2س ] ÷ حتا2س
د¯(س)
= 1÷ حتا2س
د¯(س)
= قا2س
نتيجة :
د(س) = طا[ق(س)] فإن :
د¯(س)
=
قا2[ق(س)] × ق¯(س)
رابعاً : طتا س
هنا يمكن استخدام الطريقة العادية باستخدام المبادئ الأولية
أو طتاس = حتاس ÷ حاس أو طتاس
= طا(½
ط – س) أو طتاس = 1 ÷ طاس
د(س) = طتا س
د(س) =
طا(½
ط – س)
د¯(س)
= قا2(½
ط – س) × – 1
د¯(س)
=
–
قتا2س
خامساً : قا س
د(س) = قا س
د(س) = 1 ÷ حتا س
د¯(س)
= [ حتا س × 0 – 1 × – حا س ] ÷ حتا2س
د¯(س)
= حا س ÷ حتا س جتا س
د¯(س)
= قا س طا س
سادساً : قتا س
د(س) = قتا س
د(س) = 1 ÷ حا س
د¯(س)
= [ حا س × 0 – 1 × حتا س ] ÷ حا2س
د¯(س)
= – حتا س ÷ حا س جا س
د¯(س)
= – قتا س طتا س
أو
د(س) = قتا س
د(س) = 1 ÷ حاس = حا-1س
د¯(س)
= –
حا-2س × حتا س
د¯(س)
= – حتا س ÷ حا س جا س
د¯(س)
= – قتا س طتا س