التفاضـل

القسم السادس 1

زوايا التقاطع

    الزاوية بين مستقيمين تتعين بعرفة ميلاهما وتطبيق قانون ظل الزاوية المعروف في حساب المثلثات وهنا نتكلم عن منحنيات بإيجاد الزاوية بين منحنيين أو مستقيم ومنحنى

تعريف : الزاوية التي يتقاطع عليها منحنيان عند أي نقطة مشتركة بينهما هي الزاوية الحادة المحصورة بين المماسين للمنحنين عند هذه النقطة.

    ولكل مماس ميل عند نقطة على المنحنى فتقاطع منحنيين عند نقطة يعني وجود مماسين عند تلك النقطة ميلاهما م₁ ، م₂ ويحصران بينهم زاوية والمطلوب معرفة قيمة هذه الزاوية والتي تعرف بزاوية التقاطع والشكل التالي يبين ذلك مع ملاحظة أصل قانون طاهـ كالآتي :

    هـ = ى + هـ₂     الزاوية الخارجة عن المثلث

    هـ = (180 – هـ₁ ) + هـ₂      الزاوية المستقيمة 180^ه  أي  ى = 180 – هـ₁

    هـ = 180 – هـ₁ + هـ₂            بإزالة القوس

    هـ = 180 – ( هـ₁ – هـ₂ )     بأخذ –1 عامل مشترك       

 طاهـ = طا[180 – ( هـ₁ – هـ₂ )]

 طاهـ = طا( هـ₁ – هـ₂ )    وبوضع  م₁= طاهـ₁ ،  م₂= طاهـ₂  ،  حيث نعلم بأن ميل المماس هو ظل الزاوية كما سبق ذكر ذلك

لاحظ أنَّ : هـ = 0^ه  فإن طاهـ = 0 أي م₁ –  م₂ = 0 أي م₁ = م₂  وهو شرط توازي مستقيمين

كمـا أن هـ =90^ه فإن طاهـ = ¥ أي  1 + م₁ م₂ = 0 أي م₁ م₂ =  – 1 وهو شرط تعامد مستقيمين 

مثال : أوجد زوايا تقطع المنحنى ص = س² مع المستقيم ص – س – 2 = 0

الحل :

    من معادلة المستقيم نجعل ص في الطرف الأيمن وننقل س ، 1 للطرف الأيسر فنحصل على  ص = س + 2 فيكون لدينا

    ص =  س²      ............. (1)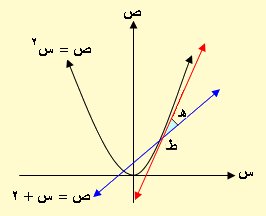

    ص =  س + 2 .............. (2)

بحل المعادلتين نحصل على نقاط التقاطع كما يلي :

    س² = س + 2    لتساوي الطرف الأيمن في المعادلتين أو بالتعويض عن ص

    س² –  س – 2 = 0      بنقل س ، 2 للطرف الأيمن

    ( س + 1 )( س – 2 ) = 0     بتحليل الطرف الأيمن

    س + 1 = 0 أو س – 2 = 0   أحد القوسين صفر أو كلاهما

    س = – 1  أو س = 2 وبالتعويض في (2) نحصل على

    ص = 1  أو  ص = 4  فتكون نقاطع تقاطع المنحنيين هي ( – 1 ، 1 ) ، ( 2 ، 4 )

نحصل على الميل باشتقاق (1) ، (2)  والتعويض عن قيم س كما يلي

    من (1) نجد أن:  ص¯ = 2 س ............. (3)

    من (2) نجد أن:  ص¯ = 1 .................. (4)    

نوجد م₁ ، م₂ عند النقطة  ( – 1 ، 1 )  بالتعويض في (3) ، (4)

    م₁ = 2 × – 1 = –2 

    م₂ = 1  وعليه نحسب الزاوية هـ المطلوبة عند ( –1 ، 1) كما يلي

  هـ = 71.6^ه  والزاوية المكملة لها  180^ه – 71.6^ه = 108.4^ه  ضرورة تحديد المكملة

تنبيه: قد يكون من الأفضل وضع ± في قانون طاهـ ليكون الناتج ± 3  فالزاوية الحادة ظلها 3 والمكملة لها – 3

نوجد م₁ ، م₂ عند النقطة  ( 2 ، 4 )  بالتعويض في (3) ، (4)

    م₁ = 2 × 2 = 4

    م₂ = 1  وعليه نحسب الزاوية هـ المطلوبة عند ( 2 ، 4 ) كما يلي:

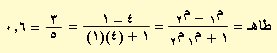
  هـ = 31^ه  والزاوية المكملة لها  180^ه – 31^ه = 149^ه

مثال 2 : أوجد زوايا التقاطع للمنحنيين س² +  ص²  – 34 = 0  ،  س² – ص – 4 = 0

الحــل :

نحل المعادلتين للحصول على نقاط التقاطع بوضعهم بالصورة :

    س² =  – ص² + 34 ............ (1)

    س² =  ص + 4  ................ (2)

من (1) ، (2) نجد أن :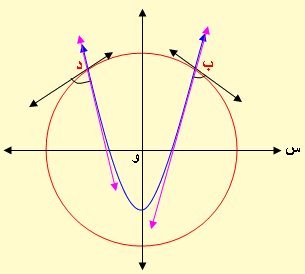

  – ص² + 34 =  ص + 4  بتساوي الطرف الأيسر

    ص²+ ص – 30 = 0        نحلل

    (ص + 6)(ص – 5) = 0   

    ص = – 6 أو ص = 5  وبالتعويض في المعادلة (2) نجد أن :

ص = – 6     فإنَّ :        س² = – 6 + 4 = – 2      أي س تخيلية فترفض

ص = 5        فإنَّ :        س² = 5 + 4 = 9      أي  س = ± 3

نقاطع التقاطع هي : ( 3 ، 5 ) ، ( – 3 ، 5 )

نوجد الميل بحساب المشتقة الأولى لكل من المنحنيين

من (1) : 2س = – 2ص ص¯    أي  س = – ص ص¯  ........ (3)

من (2) : 2 س =  ص¯   ............. (4)

عند النقطة ب(3 ، 5) وبالتعويض

في (3)     3 =  – 5 ص¯   أي  ص¯ =  – 0.6  أي   م₁ =  – 0.6

في (4)     2 × 3 =  ص¯  أي  ص¯ = 6   أي   م₂ = 6

وبالتعويض في قانون طاهـ يكون :   

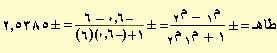
  هـ = 68.5^ه  والزاوية المكملة لها  180^ه – 68.5^ه = 111.5^ه

عند النقطة د( –3 ، 5) وبالتعويض

في (3)     –3 =  – 5 ص¯   أي  ص¯ = 0.6  أي   م₁ = 0.6

في (4)     2 × –3 =  ص¯  أي  ص¯ = – 6   أي   م₂ = – 6

وبالتعويض في قانون طاهـ يكون :

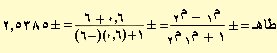
  هـ = 68.5^ه  والزاوية المكملة لها  180^ه – 68.5^ه = 111.5^ه    

تمرين1: أوجد زوايا تقاطع المنحنيين  س² + ص² = 25  ،  س² + ص² – 12 س + 11 = 0   ( الجواب 37.73 ، 37.73)

تمرين2: أوجد زوايا تقاطع المنحنيين  ص = س³ – 4 س  مع محور السينات     (الجواب 50.13 ، 82.88 ، 82.88 )