التفاضـل

القسم السادس

التطبيق الهندسي للمشتقة

    سوف نستعرض هنا في كيفية أيجاد معادلتي المماس والعمودي ، زاويا التقاطع وتحت المماس والعمودي ولا بد من القول مما سبق بأن

•  ميل منحنى الدالة عند نقطة على المنحنى هو قيمة المشتقة الأولى للدالة عند هذه النقطة.

• ميل المنحى عند أي نقطة عليه هو ميل المماس للمنحنى عند هذه النقطة.

• لإيجاد ميل المماس لمنحنى عند نقطة عليه نوجد المشتقة الأولى ونعوض فيها بإحداثي النقطة.

• العمودي على منحنى عند نقطة عليه هو العمودي على المماس عند تلك النقطة.

• لإيجاد ميل العمودي نوجد ميل المماس(ص¯) ومنه ميل العمودي = –1 ÷  ص¯  حسب شرط التعامد( م₁ × م₂ = – 1 ).

• ميل المماس = طاهـ كما سبق ذكره فإن كانت هـ حادة كان الميل موجب ، هـ منفرجة كان الميل سالب

• تحرك نقطة على منحنى يعنى اتجاه حركتها عند نقطة هو اتجاه المماس للمنحنى عند تلك النقطة

• اتجاه منحنى عند نقطه عليه هو اتجاه المماس عند تلك النقطة

• لإيجاد معادلة المماس لمنحنى عند (س₁ ، ص₁) نوجد قيمة المشتقة الأولى(م) ونستخدم ص – ص₁ = م( س – س₁).

• لإيجاد معادلة العمودي لمنحنى عند (س₁ ، ص₁) نوجد قيمة المشتقة الأولى(م)  ونستخدم ص – ص₁ = (–1÷ م)( س – س₁).

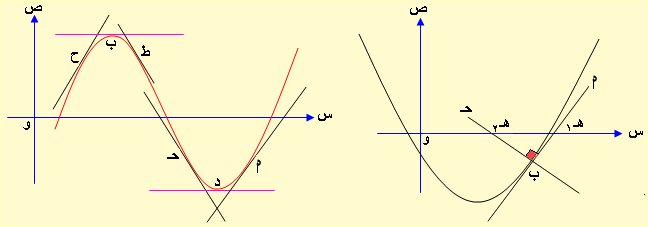
الشكل الآتي يوضح المماس والعمودي وإشارة المشتقة الأولى

    في الجزء الأيمن من الشكل أ ب مماس يميل بزاوية هـ₁ حادة على الاتجاه الموجب لمحور السينات فالميل موجب ، ب حـ عمودي يميل بزاوية هـ₂ منفرجة على الاتجاه الموجب لمحور الصادات فالميل سالب.

    في الجزء الأيسر من الشكل نجد أن ميل المماسان عند ح، أ موجب في حين ميل المماسات عند ط، حـ سالب بينما المماسات عند ب، د موازيه لمحور السينات فالميل هنا يساوي الصفر لكون ميل المحور السيني يساوي الصفر(لاحظ : إن وجد مماساً يوازي محور الصادات فيكون ميله مساوي مالانهاية لكون ميل المحور الصادي يساوي مالانهاية كما سبق ذكره).

مثال(1) : أوجد معادلتي المماس والعمودي  للمنحنى ص = س³ + 3 س – 2 عند النقطة ( 1، 2 )

الحـل : نوجد المشتقة الأولى : ص¯ = 3 س² + 3

نوجد قيمة المشتقة(ميل المماس م) [ص¯] _س=1 = 3 × 1 + 3 = 6  وهي قيمة ميل المماس عند النقطة (م = 6 )

معادلة المماس هي :

    ص – ص₁ = م ( س – س₁ )

    ص – 2 = 6 ( س – 1 )

    ص – 2 = 6 س – 6

6 س – ص – 4 = 0

معادلة العمودي (ميله = – 1 ÷ 6 )

    ص –  ص₁ = (– 1 ÷ م )( س – س₁)

    ص – 2 = ( – 1 ÷ 6)( س – 1 )

    6 ص – 12 = – س + 1

    س + 6 ص – 13 = 0

مثال(2) :

 نقطتان دائماً على خط رأسي واحد الأولى تتحرك على المنحنى ص = 3س²–2س+7 الثانية تتحرك على المنحنى ص = ½ س² + 8س –6

أين يكون اتجاه حركة النقطة الأولى موازياً اتجاه حركة النقطة الثانية?

الحـــل :

الفكرة :

النقط الواقعة على خط رأسي واحد تكون لها نفس قيمة ألإحداثي السيني(الواقعة على خط أفقي واحد لها نفس ألإحداثي الصادي)

اتجاه حركة نقطة على المنحنى هو اتجاه المماس للمنحنى عندها والميل عندها هو المشتقة الأولى.

توازي المماسان يعني تساوي ميلاهما.

بناء على ما ورد نقول :

ميل المماس للمنحى عند النقطة الأولى هو ص¯ = 6 س – 2 وليكن م₁

ميل المماس للمنحى عند النقطة الثانية هو ص¯ =  س + 8  وليكن م₂

لكونهم متوازيان يكون : 6 س –  2 = س + 8  ومنها س = 2

النقطة الأولى : بالتعويض في المنحنى الأول يكون  ص = 12 – 4 + 7 = 7 فالنقطة ( 2 ، 15 )

النقطة الثانية : بالتعويض في المنحنى الثاني  يكون ص = 2 + 16– 6 = 7 فالنقطة ( 2 ، 12 )

مثال(3) :

أوجد النقط الواقعة على المنحنى  س² + ص² + 3 س + ص = 0 والتي يكون  المماس عندها عمودياً على المستقيم  س +  3 ص + 4 = 0

الحــل :

    هنا ميل المماس لم يعطى مباشرة بقول المماس عمودي على مستقيم وعليه نوجد ميل المستقيم ونطبق شرط التعامد للحصول على ميل المماس فيكون ميل المستقيم هو – معامل س ÷ معامل ص = – 1 ÷ 3 ويكون ميل المماس = 3 ( حسب شرط التعامد م₁ × م₂ = – 1 )

    ميل المماس هو المشتقة الأولى ( ص¯ ) أي  ص¯ = 3 ، التي يمكن الحصول عليها أيضاً باشتقاق معادلة المنحنى أي :

     س² + ص² + 3 س + ص = 0 ←(1) 

   2 س + 2 ص  ص¯  + 3 +  ص¯  = 0      ـ اشتقاق الدالة الضمنية ـ

    2 س + 2 ص × 3 + 3 + 3 = 0

    2 س + 6 ص + 6 = 0

    س + 3 ص + 3 = 0

    س = – 3 ص – 3  ←(2)   

وبالتعويض في عن قيمة س في معادلة المنحنى (1)  يكون :

    ( – 3 ص – 3 )² + ص² + 3 ( – 3 ص – 3 ) + ص = 0

    9 ص² + 18 ص + 9 + ص² – 9 ص – 9 + ص = 0

    10 ص² + 10 ص = 0

    10 ص ( ص + 1 ) = 0

    ص = 0  أو ص = – 1 وبالتعويض في المعادلة (2) لحساب قيمة س

     س = – 3 أو س = 0

    النقاط المطلوبة هي ( – 3 ، 0 ) ، ( 0 ، – 1 )

مثال(4) :
أثبت أنَّ النقطة (– 1 ، 3 ) تقع على المنحنى س2+ ص2 – 4 س + 2 ص = 20 ، ثم أوجد معادلتي المماس والعمودي عندها.
الحـل :
نعوض عن س = – 1 ، ص = 3 في الطرف الأيمن من لمعادلة المنحى فإن كان الناتج 20 فالنقطة واقعة على المنحنى
الطرف الأيمن = 1 + 9 + 4 + 6 = 20 = الطرف الأيسر فالنقطة تقع على المنحنى
لإيجاد المعادلة نوجد الميل ، ميل المماس = المشتقة الأولى عند النقطة ، وميل العمودي مقلوب ميل المماس بإشارة مخالفة
2 س + 2 ص ص¯ – 4 + 2 ص¯ = 0 باشتقاق معادلة المنحنى بالنسبة إلى س
2 × – 1 + 2 × 3 ص¯ – 4 + 2 ص¯ = 0 بالتعويض من النقطة
– 6 + 8 ص¯ = 0 ومنها ص¯ = 3 ÷ 4 أي ميل المماس م = 3 ÷ 4 فالمعادلة تكون
ص – ص1 = م ( س – س1 )
ص – 3 = (3 ÷ 4) ( س – (–1)) بالضرب في 4
4 ص – 12 = 3 س + 3
3 س – 4 ص + 15 = 0 وهي معادلة المماس
حيث أن ميل المماس م = 3 ÷ 4 فإنَّ ميل العمودي(العمودي على المماس عند النقطة) = – 4 ÷ 3 فمعادلته هي
ص – ص1 = م ( س – س1 )
ص – 3 = (– 4 ÷ 3) ( س – (–1)) وبالضرب × 3
3 ص – 9 = – 4 س – 4
4 س + 3 ص – 5 = 0

تمارين :

1) أوجد النقط على المنحنى 3 ص = س³ – 3 س² – 1 والتي يصنع عندها المماس مع الاتجاه الموجب لمحور السينات زاوية قياسها 135^ه  وكذلك

    النقط التي يكون عندها المماس مواز لمحور السينات

2) أوجد النقط على المنحنى ص = ½ س³ – ½ س² + 11 والتي تكون المماسات عندها موازية المستقيم س – 2 ص – 1 = 0

3) أوجد معادلات المماسات للمنحنى س³ + 2 ص² – 9 = 0 عند النقط التي إحداثياتها السينية = 1

  4) إذا كان المستقيم 3 س – 2 ص – حـ = 0 يمس المنحنى ص² = 4 س فأوجد نقطة التماس ومن ثم أستنتج قيمة حـ.

  5) إذا كان المستقيم س – حـ ص + 2 = 0 يمس المنحنى ص³ = 8 س فأثبت أن هناك قيمتين للمتغير حـ وأوجدهم وأثبت أن المماسين عندهم

       متعامدين وأوجد نقطتي التماس.