التفاضـل

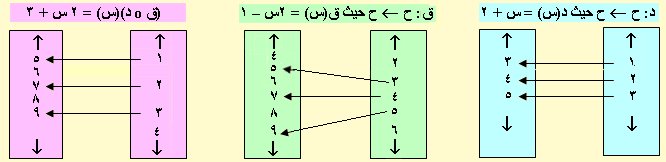
لكل دالة مجال ومجال مقابل وقاعدة اقتران ومفهوم تركيب دالتين هو الحصول على دالة منهم كحال 2، 3 مع الجمع العادي لنحصل على 5، وهذا يعني وجود عملية تجعل الدالتين دالة واحدة ويرمز لها بالرمز o في الغالب وتقرأ كما يحلو للبعض بدائرة فتركيب الدالتين د(س)، ق(س) يأخذ الصورة (د o ق)(ٍس) أو (ق o د)(س) وهي دالة مركبة وهما مختلفتين تماما ًوتسمى كل منها بدالة الدالة أو الدالة المركبة ويشترط أن يكون مدى د مجموعة جزئية من مجال ق للدالة (ق o د)(س) كما يظهر مما يأتي:

صورة العنصر 1 تحت تأثير التطبيق د هو 3 وصورة 3 تحت تأثير التطبيق ق هو 5 ويكون صورة 1 تحت تأثير قo د هو 5 أي أن (ق o د)(1) = 5 وبصورة أخرى د(1) = 3 ، ق(3) = 5 وبتركيب الدالتين ق(د(1)) = ق(3) = 5 أو بالتعويض مباشرة في (ق o د)(س) = 2 س + 3 التي نتجت مما يأتي : (ق o د)(س) = ق(د(س)) = ق(س +2) = 2(س + 2) – 1 = 2 س + 4 – 1 = 2 س + 3 فيكون :

(د o ق)(س) = د(ق(س)) = د(2س – 1) = 2س – 1 + 2 = 2س + 1 # 2س + 3 = (ق o د)(س) وهذا يعني أن العملية o ليست أبدالية

المشتقة الأولى للدالة (د o ق)(س)

نظريـة إذا كانت كل من د، ق قابلة للاشتقاق فإن: (د o ق)¯(س) = د¯(ق(س)) × ق¯(س) وكذلك (ق o د)¯(س) = ق¯(د(س)) × د¯(س)

مثال : إذا كانت د(س) = س + 2 ، ق(س) = 2س² – 3 فأوجد المشتقة الأولى للدالة (ق o د)(س)

الحل : يمكن الحل هنا بطريقتين التعويض ثم الاشتقاق أو الاشتقاق ثم التعويض وسنسرد الطريقتين

الطريقة الأولى : التعويض (ق o د)(س) = ق(د(س)) = ق(س + 2) = 2(س + 2)² – 3 = 2( س² + 4 س + 4) – 3 = 2س² + 8 س + 5

الطريقة الثانية : بالاشتقاق يكون: د¯(س) = 1 ، ق¯(س) = 4 س

هناك ما يعرف بقاعدة التسلسل بأن نوجد مشتقة ص بالنسبة إلى ع وكذلك مشتقة ع بالنسبة إلى س فناتج ضربهم يكون مشتقة ص بالنسبة إلى س

إذا كانت ص = د(ع) ، ع = د(س) فيمكن حذف ع للحصول على علاقة مباشرة بين ص ، س يسهل اشتقاقها مثل :

ص¯= 18 س + 15 أو استخدام قاعدة التسلسل كالآتي :

وهذا نفس الناتج السابق حيث بدأنا بالتعويض ثم الاشتقاق وهنا العكس الاشتقاق ثم التعويض