التفاضـل

القسم الأول

التغير ـ متوسط التغير ـ المعنى الهندسي لمتوسط التغير ـ معدل التغير(لدالة)

التغير:ـ

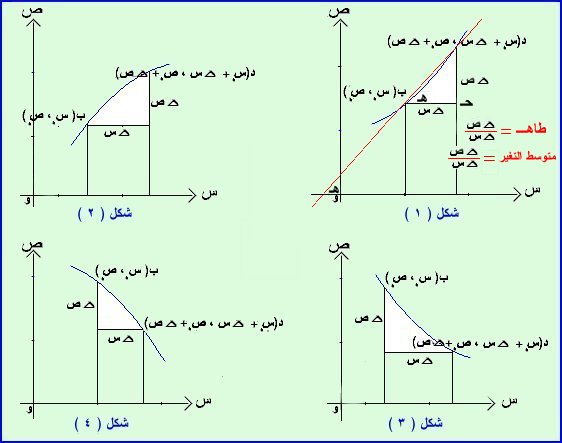
    في دراستنا للعلوم المختلفة نلاحظ وجود علاقة بين المتغيرات التي يمكن التعبير عنها بصورة دالة وهدفنا البحث عن العلاقة بين ما يحدث من تغير للدالة بناء على التغير في المتغير المستقل وكذلك الحال لدالة متوسط تغير الدالة بالنسبة لمتغيرها المستقل وما يترتب على ذلك من استنتاجات مفيدة عملياً. فبحثنا في الدالة ص =  د(س) = س2 (يكفي كتابة ص أو د(س) ) فكون س تغيرت من 1 إلى 2 مثلاً فقيمة التغير في س = 2 ـ 1 = 1 ويكون التغير المناظر في ص = (2)2 ـ (1)2 = 4 ـ 1 = 3 ويرمز للتغير في س بالرمز ∆ س ويقرأ دلتا س حيث دلنا تعني بالعربية التغير في وذكرنا ∆ س يعني الجملة العربية " التغير في س " ، ∆ س رمز واحد للتغير في س ولا يعني شيء فصل ∆ عن س فمثلاً  س × ∆ س لا يساوي ∆ س2 إطلاقاً وكذلك للتغير في ص نرمز له ∆ ص وعلى العموم تغير س من س1 إلى س2 الذي يتبعه تغير ص من ص1 إلى ص2  حيث س المتغير المستقل ، ص المتغير التابع فيكون: ∆ س = س2 ـ س1 ، ∆ ص = ص2 ـ ص1 والتغير في س دال على التغير في قيمتها بالزيادة أو النقص والحال نفسه مع ص وعليه فقد يكون التغير في س ، ص موجباً أو سالباً، الأشكال الأربع التالية توضح تمثيلاً بيانياً للمقدارين ∆ س ، ∆ ص وذلك للدالة ص =  د(س) ، حيث ب (س0 ، ص0) ، د (س0 + ∆ س ، ص0 + ∆ ص) ففي الشكلين (1 ، 2) تزيد قيمة ص بزيادة قيمة س ولذا تكون ∆ س ، ∆ ص موجبة وفي الشكلين (3 ، 4) نجد أن ص تنقص بزيادة س ولذا تكون ∆ س موجبة في حين ∆ ص سالبة.

متوسط التغير في دالة :ـ

    عندما تتغير س من س1 إلى س2 تتغير ص من ص1 إلى ص2 وتكون: ∆ س = س2 ـ س1  ،   ∆ ص = ص2 ـ ص1 للدالة التي ندرسها وصورتها  ص =  د(س) ومتوسط تغير الدالة ص بالنسبة لمتغيرها المستقل س يكون:

فإذا أخذنا الدالة ص = س2 ، س1= 2 ، س2 = 3 ، ص = س2 فإن :  د(س1) = د(2) = 2 2 = 4  ،  د(س2) = د(3) = 3 2 = 9

∆ ص =  د(3) ـ د(2) = 9 ـ 4 = 5  ،   ∆ س = 3 ـ 2 = 1

أي أن مقدار متوسط التغير هنا = 5 ÷ 1 = 5

وعلى وجه العموم لدالة المتغير الواحد ص = د(س) فكل تغير في س قدره ∆ س يحدث تغير مناظر له في ص قدره ∆ ص فإذا أخذنا قيمة ابتدائية مثل ب(س0 ، ص0) فإن

ص0 = د( س0)  ......................................... (1)

ص0 +  ∆ ص = د( س0 +  ∆ س)   ............... (2)

    وبطرح (1) من (2) يكون :

 ∆ ص = د( س0 +  ∆ س) ـ د( س0)

    وبالقسمة على  ∆ س حيث  ∆ س ≠ 0 يكون متوسط تغير الدالة في الفترة من س0 إلى  س0 + ∆ س

المعنى الهندسي لمتوسط التغير لدالة

   

       في شكل(1) السابق ب حـ يمثل ∆ س ، د حـ يمثل ∆ ص النقطة ب(س0 ، ص0) على المنحنى  سنبدأ منها قياس التغير للدالة ولنأخذ النقطة الأخرى د( س0 +  ∆ س ، ص0 +  ∆ ص) فيكون ميل القاطع(الوتر للمنحنى) ب د هو ظل الزاوية(هـ) التي يصنعها مع الاتجاه الموجب لمحور السينات حسب تعريف ميل المستقيم ويساوي المقابل ÷ المجاور أي أن متوسط التغير = طاهـ = د حـ ÷ ب حـ  = ∆ ص ÷ ∆ س وعليه يكون متوسط تغير الدالة يعبر عن ميل القاطع(الوتر) ب د

مثال : أوجد متوسط تغير الدالة ص = 2 س2 + 3 س ـ 5 في الفترة من س = 2 إلى س = 4

الحل :

        ص = 2 س2 + 3 س ـ 5  .......................................................... (1)

    ص +  ∆ ص = 2 ( س +  ∆ س)2 + 3( س +  ∆ س) ـ 5

    ص +  ∆ ص = 2 ( س2 + 2 س .  ∆ س + ( ∆ س)2 ) + 3 س + 3 ∆ س ـ 5

    ص +  ∆ ص = 2 س2 + 4 س . ∆ س + 2( ∆ س)2 + 3 س + 3 ∆ س ـ 5  ............ (2)

     بطرح (1) من (2)

     ∆ ص = 4 س .  ∆ س + 3 ∆ س + 2( ∆ س)2

     ∆ ص = ( 4 س + 3 ) ∆ س + 2(∆ س)2

    بالقسمة على ∆ س

    متوسط التغير = (4 س + 3) + 2 ∆ س

    حيث أن س = 2 ، ∆ س = 4 - 2 = 2

    متوسط التغير = 4 × 2 + 3 + 2 × 2

    متوسط التغير = 15

 

معدل التغير لدالة

 

    معدل تغير دالة بالنسبة لمتغيرها المستقل ، فإذا نظرنا لشكل (1) وثبتنا النقطة ب وتركنا النقطة د تتحرك على المنحنى مقتربة من النقطة ب فمن المؤكد أن قيمة ∆ س تصغر تدريجياً وكذلك ∆ ص تصغر ويمكن حساب قيمة كل من ∆ س ، ∆ ص عند كل موضع وحساب متوسط التغير للدالة وذلك  بقسمة ∆ ص على ∆ س والجدول التالي يبين ذلك للمنحنى ص = س2 ، ∆ س تبدأ بالقيمة 1 ثم تتناقص في النصف الأول من الجدول كقيمة موجبة في حين ∆ س تبدأ بالقيمة ـ1 ثم تتزايد في النصف الثاني من الجدول كقيمة سالبة بهدف الاقتراب قيمة س0+ ∆ س من 2 فيقترب متوسط التغير من 4

متوسط التغير ∆ ص = د(س0 + ∆ س) ـ د(س0) د(س0 + ∆ س) د(س0) ∆ س س0 + ∆ س

س0
5 5 9 4 1 3 2
4.5 2.25 6.25 4 0.5 2.5 2
4.2 0.84 4.84 4 0.2 2.2 2
4.1 0.41 4.41 4 0.1 2.1 2
4.01 0.0401 4.0401 4 0.01 2.01 2
4.001 0.004001 4.004001 4 0.001 2.001 2
4.0001 0.00040001 4.00040001 4 0.0001 2.0001 2
â â â â â â â
4 صفر 4 4 صفر 2 2
á á á á á á á
3.9999 -0.00039999 3.99960001 4 -0.0001 1.9999 2
3.999 -0.003999 3.9996001 4 -0.001 1.999 2
3.99 -0.0399 3.9601 4 -0.01 1.99 2
3.9 -0.39 3.61 4 -0.1 1.9 2
3.8 -0.76 3.24 4 -0.2 1.8 2
3.5 -1.75 2.25 4 -0.5 1.5 2
3 -3 1 4 -1 1 2

    كلما صغرت قيمة ∆ س فإن قيمة متوسط التغير تتقارب من 4 وفي النهاية تؤول ∆ س للصفر عندها يؤول متوسط التغير إلى 4 هذا ويطلق على غاية متوسط التغير لدالة عندما ∆ س تؤول للصفر بمعدل التغير للدالة بالنسبة لمتغيرها المستقل أو معدل التغير اختصاراً أي أن

 

مثال : أوجد معدل تغير الدالة ص = 2 س2 + 3 س ـ 5

الحل :

        ص = 2 س2 + 3 س ـ 5  .......................................................... (1)

    ص +  ∆ ص = 2 ( س +  ∆ س)2 + 3( س +  ∆ س) ـ 5

    ص +  ∆ ص = 2 ( س2 + 2 س .  ∆ س + ( ∆ س)2 ) + 3 س + 3 ∆ س ـ 5

    ص +  ∆ ص = 2 س2 + 4 س . ∆ س + 2( ∆ س)2 + 3 س + 3 ∆ س ـ 5  ............ (2)

     بطرح (1) من (2)

     ∆ ص = 4 س .  ∆ س + 3 ∆ س + 2( ∆ س)2

     ∆ ص = ( 4 س + 3 ) ∆ س + 2(∆ س)2

    بالقسمة على ∆ س

    متوسط التغير = (4 س + 3) + 2 ∆ س

    معدل التغير هو غاية (4 س + 3 ) عندما ∆ س تؤول للصفر أ ي أن

    معدل التغير = 4 س + 3

وهذا يوصلنا لحقيقة جديدة عن الدالة ص = 2 س2 + 3 س ـ 5  وهي أن النسبة بيت التغيرين الصغيرين جداً في س ، ص لها غاية هي 4 س + 3 وذلك عندما يؤول كل من التغيرين ∆ س ، ∆ ص إلى الصفر وهذه الغاية هي دالة أيضاً للمتغير س وسميت بالدالة المشتقة أو مشتقة الدالة أو المعامل التفاضلي الأول أو تفاضل ص بالنسبة إلى س أو اختصاراً المشتقة الأولى  ومنها يمكن الحصول على المشتقة الثانية والثالثة و ... مع ملاحظة أن كل من د ص ، د س ليس مستقلاً عن الآخر فهما معاً رمز للتفاضل كالرمز دــ(س) أو ص ــ أو ص1 للمشتقة الأولى ولإيجاد معدل التغير أو المعامل التفاضلي الأول لدالة يجب أتباع الخطوات :