الاتصــال
ماذا نقصد بقولنا أن الدالة متصلة، بالطبع نعني منحنى الدالة أو الخط البياني للدالة مستمر دون انقطاع في الفترة المحددة له بالنص وهذا يعني أن كل قيمة من قيم الفترة معرفة على الدالة أو بمعنى أكثر دقة أن الدالة معرفة لجميع قيم الفترة المعطاة لهذه الدالة، فمثلاً يكون منحى الدالة
2
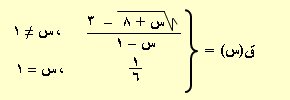
د(س) = 2س + 3 متصل في ح ومنحنى الدالة د(س) = ـــــــــــــــــ غير متصل عند س = 1 لأن الدالة غير معرفة عند س = 1 كما نعلم ، وبالطبــع
س – 1
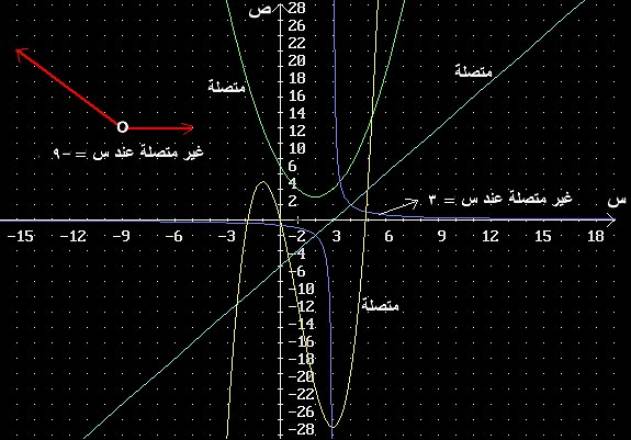
دوال كثيرات الحدود أو دوال المقياس(القيمة المطلقة) لا تسبب لنا مشكلة في اتصالها ولكن تظهر المشكلة للدوال النسبية التي يجب أن لا يكون مقامها مساوياً الصفر وإلا فالأمر يحتاج لدراسة أو الدوال المعرفة بقاعدتين مختلفتين عند نقطة فمشكلتنا عند تلك النقطة وليس ما قبلها أو ما بعدها ولذا نحتال للتعرف على اتصالها ببحث غايتها اليمنى واليسرى عند تلك النقطة فان كانا لهما نفس الناتج فمرحباً بها وإلا ... والحال لباقي الدوال الآسية واللوغاريتمية والمثلثية والاتصال في الفترات مفتوحة ومغلقة و ... ولكن تركيزنا سيكون على منهاج المرحلة الثانوية للوصول للهدف المنشود وهو التفاضل والتكامل والآن لنستعرض الشكل الآتي لمنحنيات بعض الدوال بهدف تبيان الاتصال والانفصال(عدم الاتصال)

خمسة منحنيات 3 متصلة وآخران غير متصلين
الاتصال عند نقطة لدالة Continuity of a function at a point
بكل بساطة نقول أن الدالة د(س) متصلة عند النقطة س = ل أو عند (ل ، د(ل)) إذا تحقق الآتي:
1) د(ل) موجودة أي د(ل)' ح وبمعنى أصح أن الدالة معرفة عند النقطة (ل ، د(ل))
2) غاية الدالة عندما س تؤول إلى ل= ك Э ح أن أن الغاية للدالة عند النقطة موجودة
3) تساوي الناتجان في 1) ، 2) أي أن غاية الدالة عند ل= د(ل) وقد يكتفي البعض بهذا لكونه يشمل 1) ، 2)
د(س) متصلة عند ل ↔ غـــــــــــــــــاد(س) = د(ل)
س ← ل
فمثلاً
1) الدالة د(س) = س ÷ (س – 1) متصلة في ح/{1} ويمكن القول بأن الدالة غير متصلة عند س = 1 لأن د(1) غير موجودة أي تساوي مالانهاية
التي لا تنتمي إلى ح
2) الدالة ق(س) = س2 + 5 متصلة عن س = 2 لأن غايتها عند 2 تساوي د(2) تساوي 9
( س2 + 2 ، س < 1
3) الدالة : د(س) =
( 4 س –3 ، س ≥ 1
غير متصلة عند س = 1 لأن د(1) = 1 والغاية غير موجودة فالغاية اليمنى1 والغاية اليسرى3 ولكننا نقول أن الدالة متصلة من اليمين
( س2 + 2س – 5 ، س < 2
4) الدالة : ق(س) =
( 2 س – 1 ، س ≥ 2
ق(س) متصلة عند 2 لأن ق(2) = 3 وكل من الغاية اليمنى واليسرى تساوي3 أي الغاية موجودة وتساوي ق(2)
وعلى العموم لمعرفة اتصال دالة عند نقطة ل مثلاً فيجب التأكد أن التعويض المباشر في الدالة يعطي قيمة حقيقية ومن ثم نبحث غاية الدالة ويجب أن تكون موجودة ومساوية للقيمة الحقيقية السابقة وإلا فالدالة غير متصلة
يمكن معرفة اتصال الدالة من المنحنى الخاص بها كما هو مبين بالشكل السابق
أيجاد غاية دالة هنا كما سبق ذكره في موضوع الغايات كخطوة ثانية بعد التعويض المباشر
قد يطلب بحث الاتصال من يمين النقطة فيكفي بحث الغاية اليمنى فقط بعد التأكد من وجود قيمة للدالة عند النقطة
في الدالة المعرفة بقاعدتين بعد معرفة قيمة الدالة من إحدى القاعدتين نبحث الغاية عند النقطة للقاعدة الثانية أولاً
( س2 + ك س + 1 ، س > 4
مثال: أوجد قيمة ك التي تجعل الدالة د(س) متصلة عند س = 4 حيث د(س) =
( 3 – س ، س ≤ 4
د(4) = 3 – 4 = –1
غـــــــــــــــــاد(س) = –1 لأن الدالة متصلة فالغاية اليمنى = الغاية اليسرى = د(4) = –1
س ←4
غـــــــــــــــــا(س2 + ك س + 1) = –1
س ←4+
16 + 4 ك + 1 = –1 ومنها يكون:
ك = 4.5
تمارين
ابحث اتصال الدالة د(س) عند س = ل في كل مما يأتي
(1) د(س) = | س – 1| ، ل = 1
(2) د(س) = (س + 1) ÷ ( س – 2) ، س = 3
(3) د(س) = (س + 1) ÷ ( س – 2) ، س = 2
( س2 + 2س – 5 ، س < 2
(4) الدالة: ق(س) = ، ل = 2
( 2 س + 3 ، س ≥ 2
( س2 +2 س – ل ، س ≠ 2
(5) أوجد قيمة ل التي تجعل الدالة د(س) متصلة عند س = 2 حيث د(س) =
( 3 ، س = 2
(6) ابحث اتصال الدالة الآتية عند س = 1