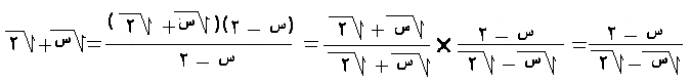الكميات
الجذرية
الكميات الجذرية لا تدخل ضمن تحليل المقادير الجبرية ولكنها تلعب
دور جيد في التفاضل ولذا ستكون محل اهتمام هنا لتسهيل عملية اختصارها في التفاضل
والكميات الجذرية في الغالب تكون من حد واحد أو حدين
نعلم
من الفرق بين مربعين س2 ـ ص2 = (س ـ ص)(س + ص) نسمي العاملين س + ص ، س ـ ص بكميتين مترافقتين
لاختلافهما فقط في الإشارة فحاصل ضربهما يساوي مربع الحد الأول ـ مربع الحد الثاني
في أي من العاملين وهذا ما يفيدنا من التخلص من الكمية الجذرية ذات الحدين إن وجدت
في مقام كسر وحال وجود حد جذري واحد في مقام كسر يكفي ضرب حدي الكسر في هذه الكمية
للتخلص من الكمية الجذرية الموجودة في المقام
|
ناتج
الضرب |
المرافق |
الكمية |
|
3 ـ 2 =
1 |
|
|
|
9×2 ـ 5 = 18 ـ 5
= 13 |
|
|
|
7 + 5 =
12 |
|
|
|
7 |
|
|
وفي
حال وجود كمية جذرية في كل من البسط والمقام لكسر يجب الضرب في مرافق كل كمية نعطي
هذا المثال لتبيان الضرب في المرافق وكما ذكرنا له دوره في التفاضل
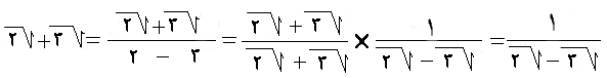
وهذا مثال آخر لتبيان سبب الضرب في المرافق حيث التعويض عن
القيمة س =
2 في الكسر لكان الناتج قيمة غير معينة وسيأتي تفصيله لاحقاً