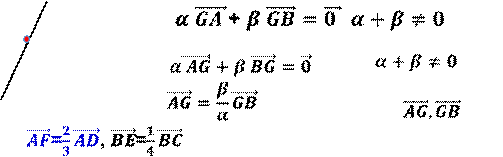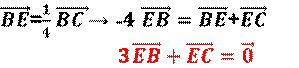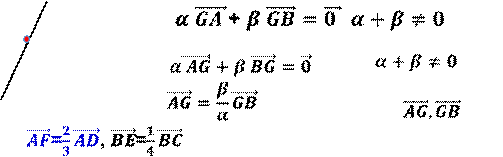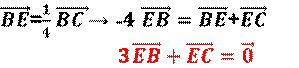مركز الأبعاد المتناسبة لثلاث نقط

مركز الأبعاد المتناسبة لنقطتين

نقول أن G مركز أبعاد متناسية للنقط المثقلة (A,α)، (B,β)، (C,γ) إذا تحققت

(B, β)

G مركز الأبعاد المتناسبة للنقطتين المثقلتين A, B إذا تحققت العلاقة:

العلاقة:

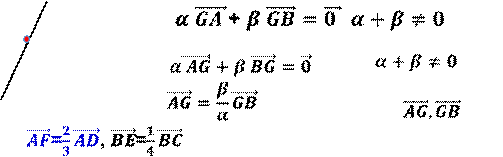
G

OR:

ومنه نجد:

(A, α)

مرتبطين خطياً

ومنه:

مرتبطة خطياً

نتأمل رباعي وجوه ABCD، ونقطتين وفق:

مثال:

والنقاط A, B, C تقع في مستوى واحد ABC

أثبت أنَّ G مركز الأبعاد المتناسبة للنقاط :

كما إن G تقع في المستوى ABC

[EF] ويقع على (A, 1)، (C, 1)، (B, 3)، (D, 2)

مثال:

الحـل:

إذا كان:

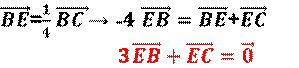
تكن G مركز الأبعاد المتناسبة للنقط الثلاثة المثقلة (A, 3)، (B, 2)، (C, -7)

(H, 5)

حسب الخاصية التجميعية:ـ

ويكون:

A

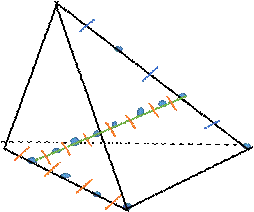
ومنه E مركز الأبعاد المتناسبة للنقطتين (B, 3) ،(C, 1)

الخاصية التجميعية

(E, 4)

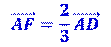
ومنه F مركز الأبعاد المتناسبة للنقطتين (A, 1) ،(D, 2)

F

(F, 3)

الخاصية التجميعية

ومنه G مركز الأبعاد المتناسبة للنقطتين

G

(F, 3)

،(E, 4)

B

D

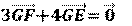
E

ومنه G يقع على [EF]

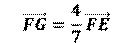
C

H

G

25 PAGE 44

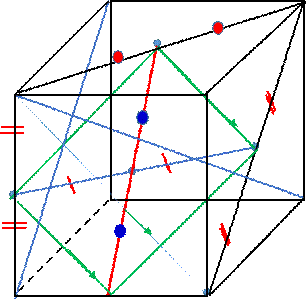
نتأمل مكعباً ABCDEFGH، والنقاط L ,K ,J ,I منتصفات [AE] ,[EG] ,[BG], [AB]

K

بالترتيب، والنقطة M مركز الأبعاد المتناسبة للنقاط (A, 1) ،(B, 1)، (G, 1)، (E, 1).

أثبت أنَّ M تنتمي إلى [IJ] وعيِّن موضعها على هذه القطعة.

E

F

أثبت أنَّ M تنتمي إلى [KL] وعيِّن موضعها على هذه القطعة.

اىستنتج أنَّ I و J و K و L تقع في مستوٍ واحد وعين طبيعة الرباعي ILJK.

J

الحـل

M

حيث I منتصف [AE]

M مركز الأبعاد المتناسبة للنقاط (A, 1) و (B, 1) و (G, 1) و (E, 1) و

I

بحسب الخاصة التجميعية

فتكون M مركز الأبعاد المتناسبة للنقاط (I, 2) و (J, 2).

D

C

أذن M منتصف  IJ و (M, 4) M وتنتمي لـ IJ وموضعها كما مبين في الشكل (في المنتصف)

بحسب الخاصة التجميعية

L منتصف  AB و (L, 2)

K منتصف  EG و (K, 2) ،

ومنه النقط I, J, K, L تقع في مستوى واحد ILJK

M منتصف  KL و (M, 4)

والشكل I L J K  متوازي أضلاع لأن القطران K L, I J ينصف كل منهما الآخر.    أو:

A

L

B

K J//E B//I L →K J // I L , ALSO: I K//A G//L J→I K//L J