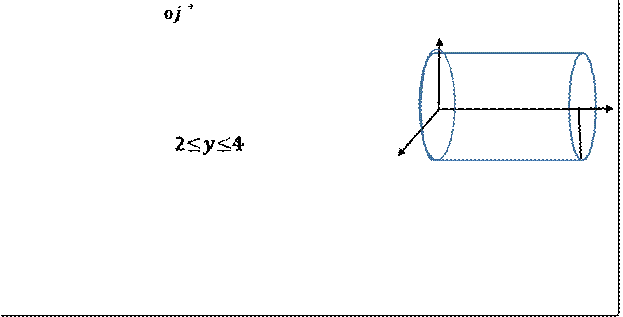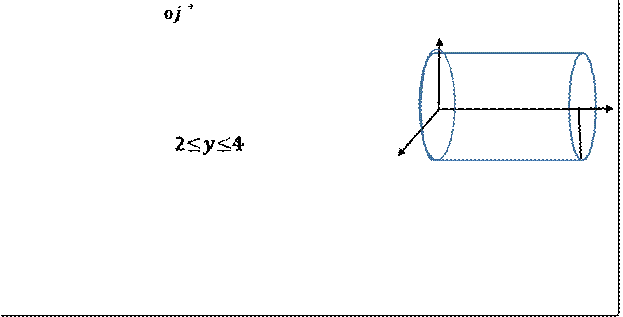(1)

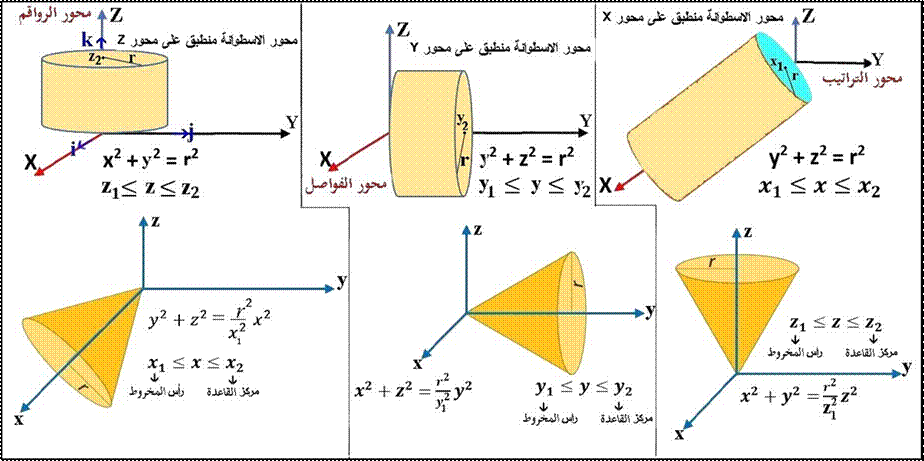
معادلتا الأسطوانة والمخروط في الفراغ

حجم الأسطوانة = π× نق²×ع

V = π r2 h

h  الارتفاع

نصف القطر r، الحجم V

A = 2 π r h, A = 2 π r h +  2 π r2

الجانبية

مساحة القاعدتبن + الجانبية

المساحة الكلية A = الجانبية + مساحة القاعدتبن

مثال:

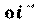
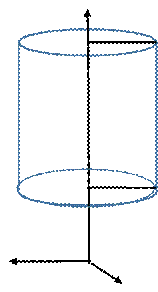
جد معادلة أسطوانة محورها (      ) ومركز قاعدنها

ونصف قطرها

T(3,0,0)

الحل:

محورها على محور السينات فمعادلتها هي:ـ

y2 +z2 = r2

y2 +z2 = 6 ،

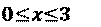
مثال:

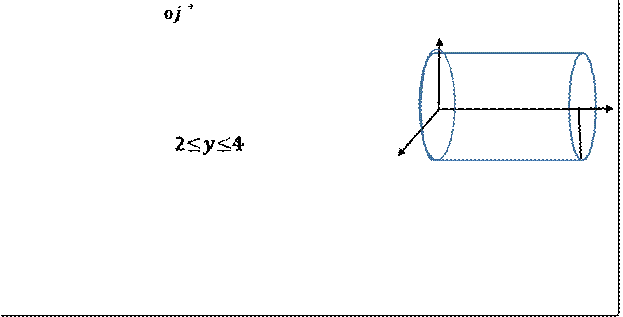
جد معادلة أسطوانة محورها (     ) ومركزا قاعدنيها

مثال:

ومركز فاعدتها (i0،0،3)A ونصف قطرها i5 , وارتفاعها i6

أسطوانة محورها (     )

r = 3 , (0 , 2, 0) , (0 , 4, 0)

Z

الحل:

11اكتب المعادلة الديكارتية للاسطوانة

الحل:

معادلتها:

محورها هو محور Z لذا

12بين ان كانت النقط الآتية تنتمي للاسطوانة

محورها على محور الصادات قمعادلتها هي:

2

2

4    y

x2 +y2 = r2

أي:

Z

B(3,4,1) , A(3,4,4)

x2 +z2 = r2

قوانين

x2 +y2 = 25

9

x2 +z2 = 9 ،

3

A(3،4،4)

9+16=25

تنتمي

8

A =

2*p*r*h=

37.7

A(3،4،1)

9+16=25

لا تنتمي

7

6

V =

p*r2*h =

56.56

A_ALL=A+2*p*r2

X

6

2B =

2pr2=56.5

A_ALL=37.7+56.5=94.2

5

المساحة الجانبية

=A

4

5

المساحة الكلية

=A_ALL

3

الحجم

=V

2

1

0

(2)

(1)

صف مجموعة النقاط التي تحقق:

Cone(O,B,3)

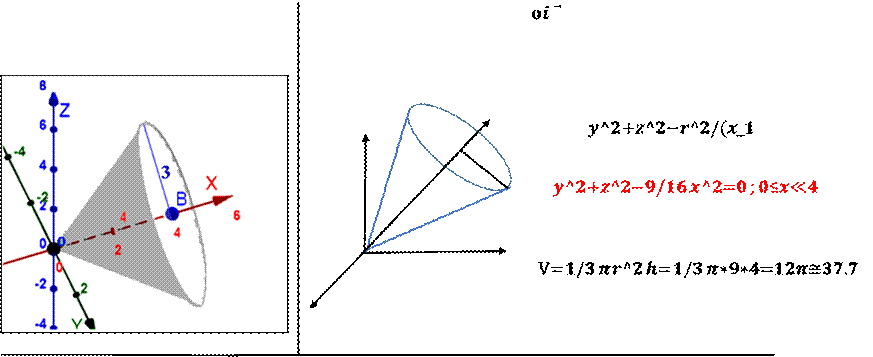
لرسم مخروط تكتب قيم B,O والأمر

وقاعدته الدائرة التي مركزها

اكتب معادلة المخروط الذي رأسه O ومحوره (     )

حيث i3 نصف قطر قاعدة المخروط.

ونصف قطرها i3 ثم أوجد مساحته الجانبية وحجمه.

B(4,0,0)

الحل:

الحل:

مجموعة النقاط تمثل مخروط رأسه O ومحوره (    )، وقاعدته

، O نقطة الأصل

r=3، x1=4

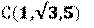
الدائرة التي مركزهاi(0,0,5) ونصف قطرها i2

x

القانون:

هل النقطة                   تقع على المخروط؟

z

B(4,0,0)

نعوض عن النقطة في معادلة المخروط

3

المعادلة:

1 + 3 -(4/25)*25=0 →1 + 3 - 4 = 0→0=0 صحيحة

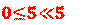
4

أنظر الشكل

النقطة C على المخروط

صحيحة

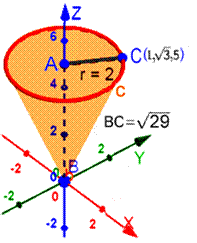
33.836

المساحة =

O

y

A =

p*r*L = p*3*5=15p ≈ 47

20.944

الحجم =

12.568

مساحة القاعدة

x

p ≈3.1416

الحجم  V

المساحة الكلية

=A_ALL

GeuGebra

Excel

A_ALL =

46.404

المساحة الكلية =